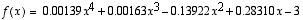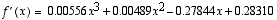Erotusosamäärä
Approbatur 1 B
Derivaatta erotusosamäärän raja-arvona
Funktion f erotusosamäärä kohdassa x0 on sama kuin kuvaajan pisteitä (x0, f(x0)) ja (x, f(x)) yhdistävän sekantin kulmakerroin. Erotusosamäärän raja-arvo, kun x → x0, on funktion derivaatta kohdassa x0:
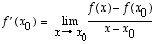
Kuvan pistettä X liikuttamalla nähdään sekantin (sininen suora) ja vastaavan erotusosamäärän muuttuminen. Kun piste X lähestyy kohtaa X0, on vastaavan erotusosamäärän raja-arvo funktion derivaatta kohdassa X0. Sekantin raja-arvona oleva tangentti saadaan painonapilla näkyviin (punainen suora). Sen kulmakerroin on siis funktion derivaatta kohdassa X0.
Tarkastelupistettä X0 voi myös liikuttaa.
Kuvassa käytetyn funktion ja sen derivaatan lausekkeet: